前陣子在做SPC逆向工程…
為此還買了一本簡體書“程序員的數學2 概率與統計”來複習一下統計的觀念
皇天不負苦心人,在經過多天的努力,最終成功的產出與“SPC參考對象”相同的結果
為了找到正確的偏移量,在此期間不知實作了多少種不同的標準差…
下一個任務是需要產生機率密度函數去看資料的離散程度…
至於什麼是常態分佈,可以到常態分佈wiki上看,應該會比我自己說還要詳細
一直很好奇為什麼要定義成鐘型,看了下面的youtube影片就才了解,這是自然界的一種規律(巧合?)
許多球從中間落下(期望值的位置),最終形成的結果接近於鐘型
上面簡介完了,接著進入主題,開始剖析標準常態分佈的機率密度函數的公式
$ f(x) = {1 \over \sqrt{2\pi}}\exp(-{x^2 \over 2}) $
如果直接從wiki看完公式後,很容易實作出來,只是我更想知道公式背後的原理
以下是我看書和上網查完資料後,根據自己理解所歸納的結果(趁印象深刻趕快記錄下來)
這時需要將公式拆成兩個部分來看
現在先看 $ f(x) = \exp(-{x^2}) $ 這部分:
為什麼要使用 $ -x^2 $ 呢?
我們知道$ x^2 $函數是開口向上的鐘型形狀,如下圖所示(以下圖片都是透過Maxima產生):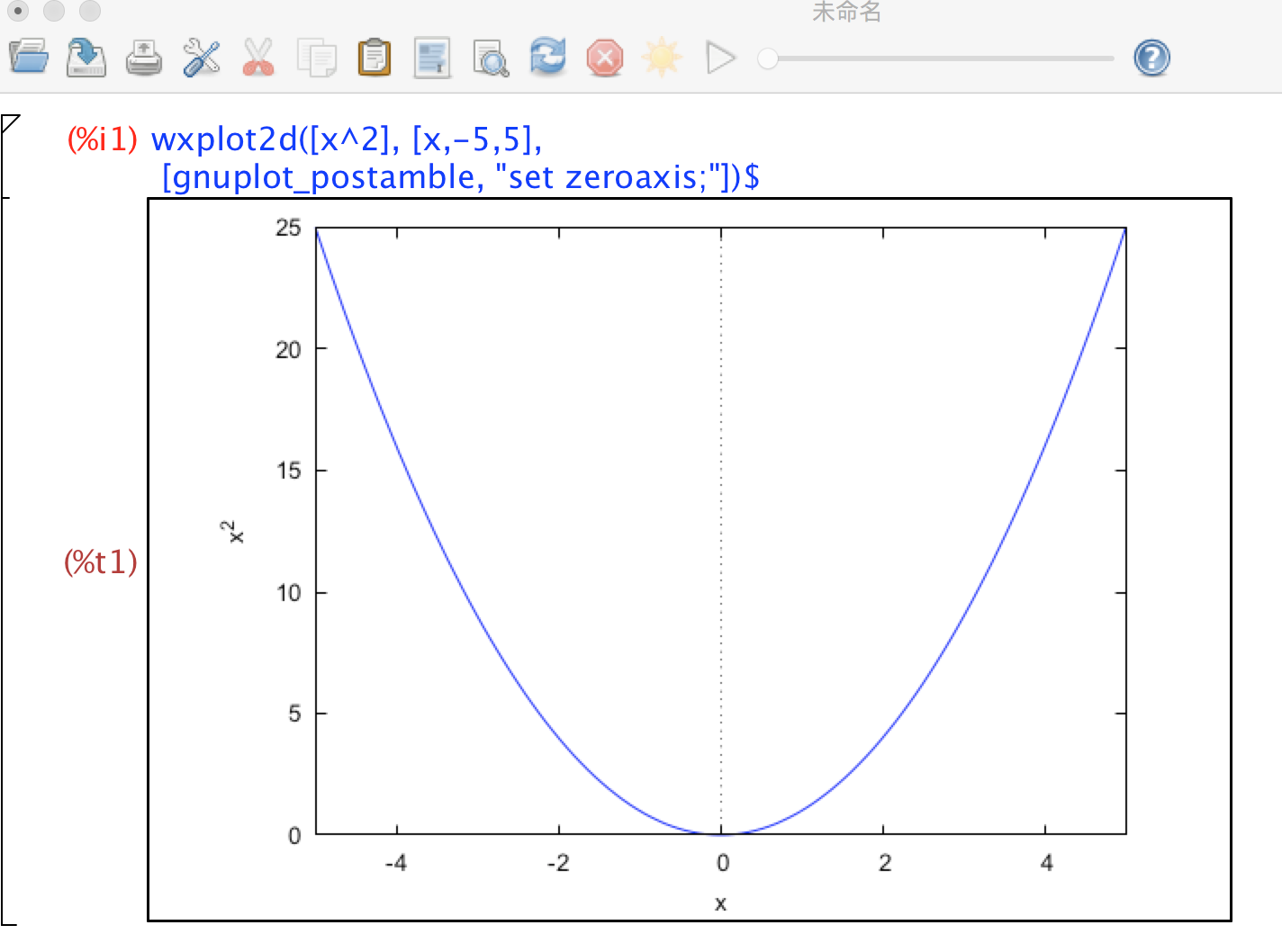
但我們要的鐘型是開口向下,想要開口向下只需要乘上-1,即 $ -x^2 $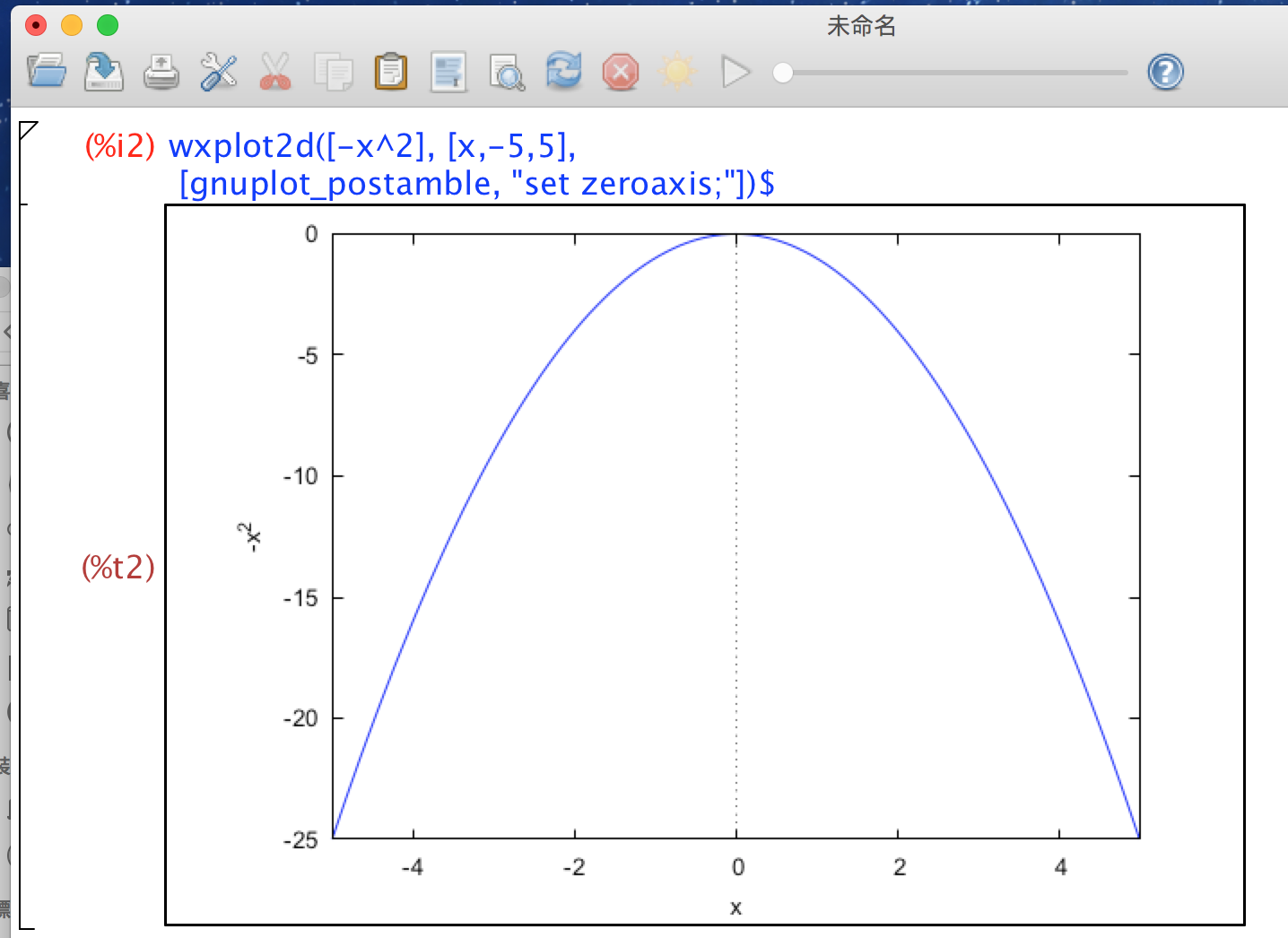
接下來看整個 $ \exp(-{x^2}) $
因為經過 $ -x^2 $ 的函數所得的的值是“恆負”的(除了頂點值為0),永遠落在第二和第三象限
但是當 $ -x^2 $ 當作常數為底的指數時,透過函數所得到的值是“恆正”的,就會落在第一和第四象限上
以下是 $ 3^{-x^2} $的函數圖形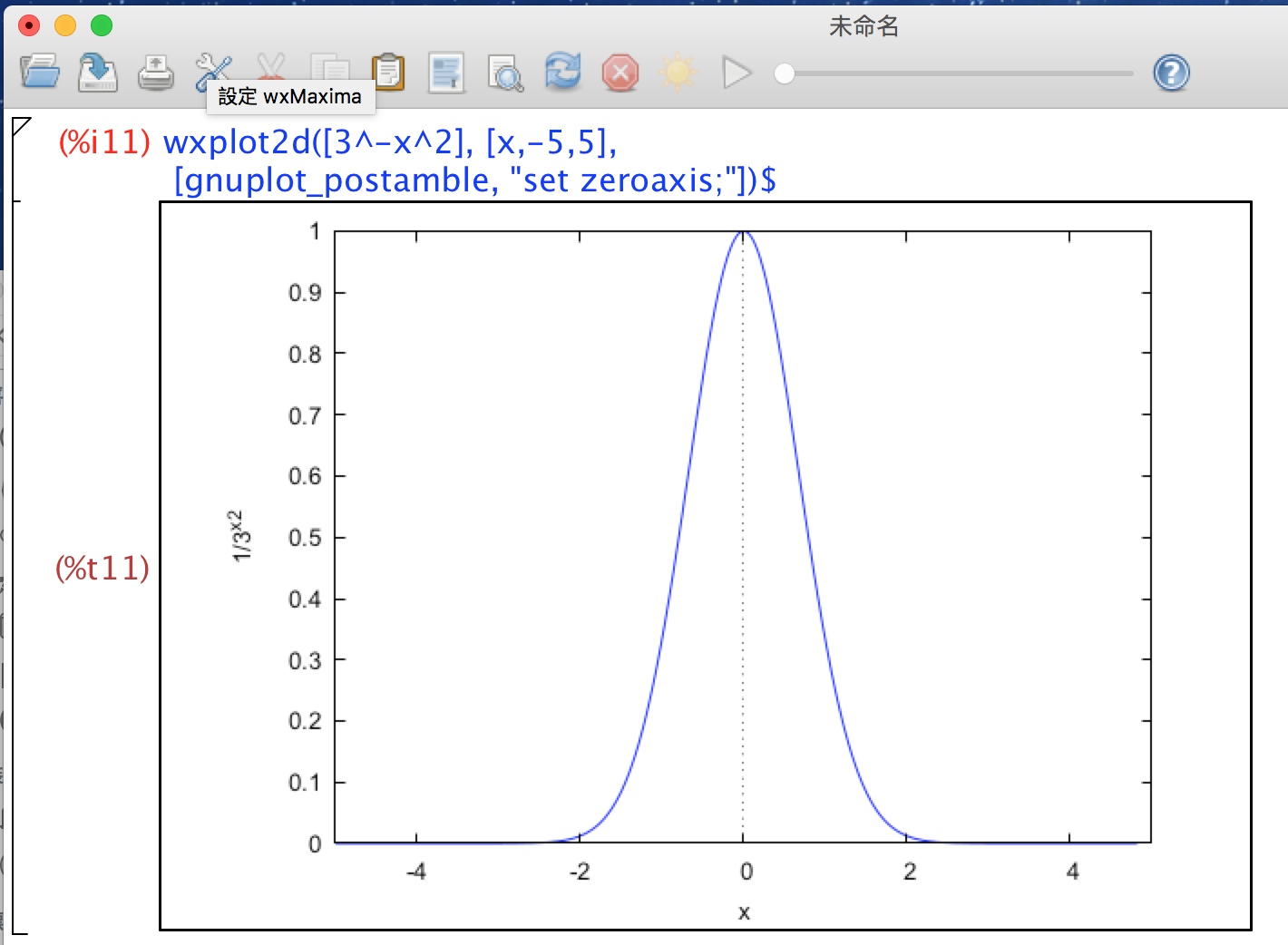
其實任何常數指數為 $ -x^2 $ 都為鐘型圖形,如下圖為$ 100^{-x^2} $的函數圖形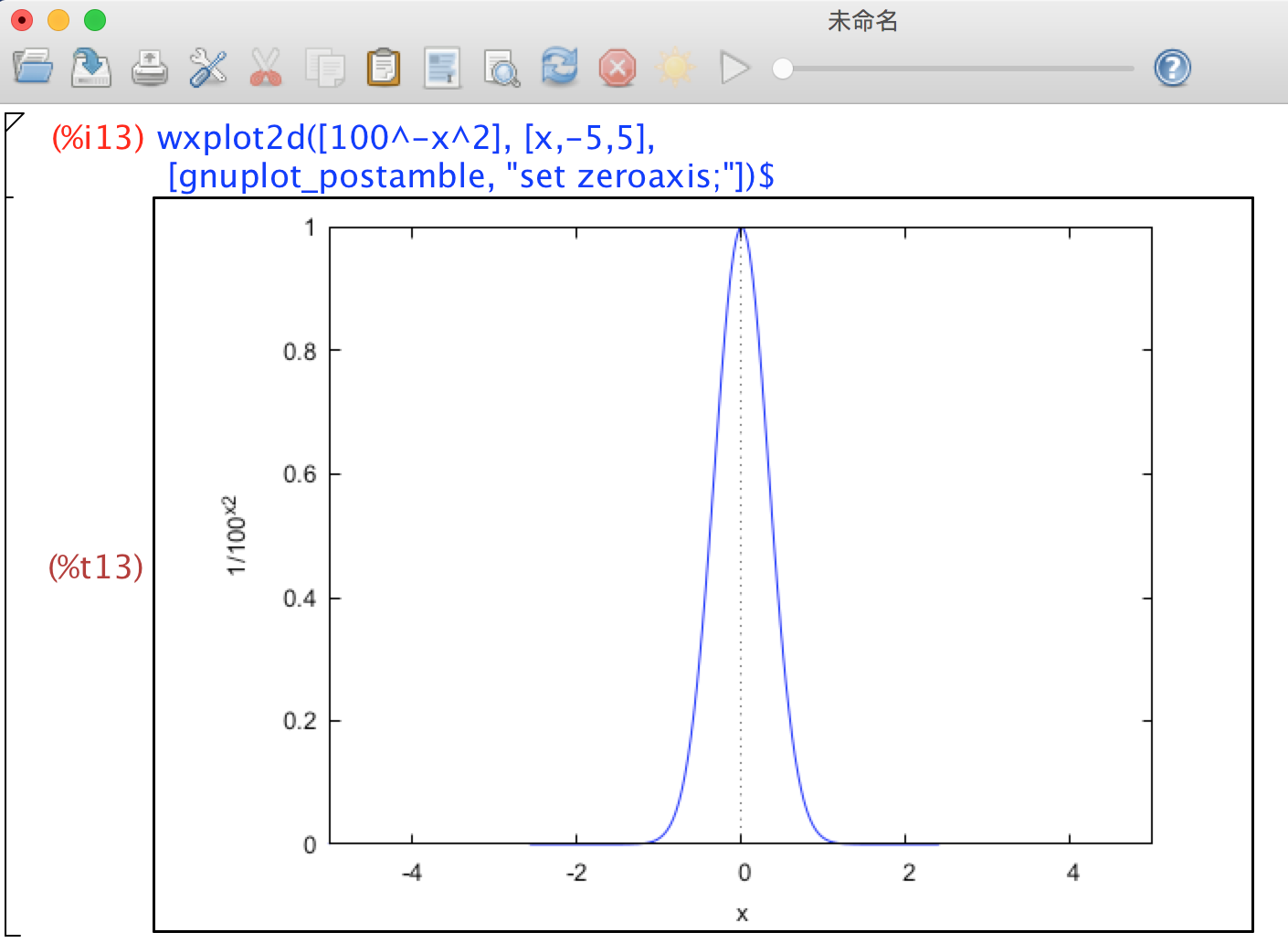
雖然取任何常數都可以形成鐘型,那為什麼要取exp當作底呢?
主要是需要它的部分特性,主要有以下五點:
- 左右對稱(以0為中心點,常數c與-c的值會得到相同值)
- x軸為0時(中心點), $ f(0) $ 會取得最大值(鐘型的最高點)
- 隨著x值逐漸遠離0時(中心點),值會漸漸縮小,且值“不會是負的”(這點很重要,因為機率值不可為負的)
- 當x趨近於無窮大或趨近於負無窮大時,值趨近於0
- 比較好做積分…(連續型的機率是透過計算面積的方式去獲得區間範圍內的機率所以要做積分)
但是只有 $ f(x) = \exp(-{x^2}) $ 是不夠的,因為對機率來說,總體 $ P(\Omega) = 1 $
所以從負無限大到無限大做積分整個 $ f(x) $的總面積必須是1
嘗試對 $ \exp(-{x^2}) $從負無窮大到無窮大做積分,得到以下結果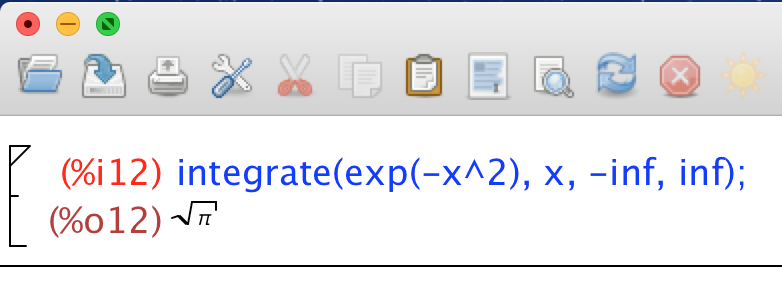
總面積會是 $ \sqrt{\pi} $ ,所以要讓值為1的方法就是除以 $ \sqrt{\pi} $
最終會得到 $ f(x) = {1 \over \sqrt{\pi}}\exp(-{x^2}) $
我們得到了常態分佈的機率密度函數,但還不能稱為“標準”常態分佈的機率密度函數
因為要達到“標準”的要求還需要有以下三個特性:
- 期望值( $ \mu $ )為0
- 變異數( $ Var $ )為1
- 標準差( $ \sigma $ )為1
記做 $ N(\mu, \sigma) $, 求 $ N(0, 1) $
但目前得到的機率分佈函數是 $ N(0, {1 \over \sqrt{2}}) = {1 \over \sqrt{\pi}}\exp(-{x^2}) $ 這不符合標準的定義,不是我們要的
我們先從wiki上看看連續型隨機變數求期望值和變異數的公式:
$ E[X] = \int xf(x)dx $
$ Var(x) = E[(x-\mu)^2] $
因為標準的期望值為0,則 $ \mu = 0 $ ,帶入後得到 $ Var(x) = E[x^2] $
先令$ g(x) = af(ax) $,其中a是一個大於零的常數,我們需要求出a值
a值需要滿足 $ \int x^2g(x) = Var(x) $ 積分等於1
$ \int x^2g(x) $ 積分後求得 $ 1 \over {2a^2} $,因為 $ {1 \over {2a^2}} = 1$
所以得到$ a = {1 \over \sqrt{2}} $可滿足 $ Var(x) = 1 $ 且 $ \mu = 0 $
也可以求得 $ \sigma = \sqrt{Var(x)} = 1 $,滿足前面所提到的三個條件
$ N(0, 1) = {1 \over \sqrt{2}} f({x \over \sqrt{2}}) $ 帶入公式後得到 $ f(x) = {1 \over \sqrt{2\pi}}\exp(-{x^2 \over 2}) $
這樣就符合“標準”常態機率密度函數
在理解後再回頭看公式,就不覺得怪了
以上所做的一切努力都是為了“湊出”滿足機率定義的函數